|
|||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||
|
Polyhedral Dice Geometry Polyhedral geometry fascinates mankind in so many ways, from young children who play with simple block cubes to scientists who study the complex geometric shapes found in nature. Maybe it's the mathematical purity found in these solids that attracts us. A fair die is one that has an equal chance of landing on any one of its faces. The mathematical term for such solid shapes is Isohedra. Each face of an Isohedra solid has the same relationship with every other face and the same relationship to the solid's centre of gravity (this includes symmetry). These shapes are also convex, so each side can rest flat and flush on an even surface. This is described as a Group structure and gives us a mathematical equation defining Isohedra known as Euler's formula - (Vertices + Faces - Sides) = 2 Not all dice are fair and some dice manufacturers have produced dice that favour some sides more than others. These may be useful as a kind of averaging die. The following geometric categories classify the main types of polyhedral dice shapes you may come across.
Regular Polyhedra The cube is one of a group of solid shapes known as Platonic Solids, named after the Greek philosopher Plato who first studied them. A better mathematical name is Regular Polyhedra. This group of solid shapes is defined by each face being a regular polygon (all sides and angles equal) and with each vertex (corner) having an equal arrangement and number of faces, all at equal angles. Regular Polyhedra make great dice because each face has an equal chance of being thrown as any other and can be considered as fair dice. There are only five of these Regular Polyhedra solid shapes that meet the above criteria. Tetrahedron, Hexahedron (Cube), Octahedron, Dodecahedron, Icosahedron.
Tetrahedrons have 4 faces and each face is an equilateral triangle (all
3 sides and angles equal). It is the only Regular Polyhedra that doesn't
have faces arranged in pairs, with every face having a directly opposite
one at a right angle. This means there isn't a side that faces upward when
it comes to rest on a flat surface. Tetrahedron dice are often marked or
numbered in each corner of each
Hexahedrons or Cubes, of course, have 6 square faces.
Octahedrons have 8 faces and each face is an equilateral triangle. Opposite faces usually add up to 9.
Dodecahedrons have 12 pentagonal faces with each face having 5 equal sides with equal angles.
Duality Hexahedrons/cubes have 6 faces and 8 vertices (corners) while Octahedrons have 8 faces and 6 vertices. Dodecahedrons have 12 faces and 20 vertices while Icosahedrons have 20 faces and 12 vertices. The converse relationship between faces and vertices is expressed as a concept known as duality. Dodecahdrons are dual with Icosahedrons. Hexahedrons/cubes are dual with Octahedrons. Tetrahedrons have 5 vertices and are dual with themselves. If you look at the illustration below you can see that each shape's vertices intersect and protrude through the centre of their dual's faces.
Prisms And Anti-Prisms Two more types of solid have identical vertices made of polygons - Prisms and Anti-Prisms. There are an infinite possible number of these shapes with the top and bottom faces made up of regular polygons with any number of sides.
Dipyramids Dipyramids are made of triangles arranged around either side of an
equator. They are dual to Prisms and make fair dice. These
shapes must have an even number of faces on each side of the equatorial line so
one face lands face-up, so Dipyramid dice come with sides numbering 8, 12, 16, 20, 24... and so on.
Trapezohedra Similar to Dipyramids are Trapezohedra with all the same, "kite" shaped,
quadrilateral faces arranged either side of an equator. They are
dual to Anti Prisms and make fair dice. These shapes must have an odd
number of faces either side of the equatorial line so one lands face-up,
so Trapezohedra dice come with sides
numbering 6, 10, 14, 18, 22... and so on.
Rhombic Triacontahedron
This shape has 30 identical
"diamond" shaped faces. It's dual is the Icosadodecahedron. Dice
of this shape aren't
Isosceles Tetrahedron
There are more possible dice shapes and some have been commercially manufactured. These solids will be featured in the future.
Some related pages for polyhedral dice are... .
|
||||||||||||||||||||||||||||||||||||||||||||
|
Copyright © 2022 Stormdark I.P. and Media. All rights reserved.
www.dice-play.com This site is for
personal use only and content may not be copied or reproduced in any form for any
purpose. Terms &
Conditions
Advertising
UK sports betting sites not on gamstop
|
|||||||||||||||||||||||||||||||||||||||||||||


 triangular face and it is the 3 numbers in
the upright position on 3 faces that
triangular face and it is the 3 numbers in
the upright position on 3 faces that determines the outcome of a throw.
Some tetrahedron dice are numbered centrally along each base line and
are read by taking the numbers in the upright position along the base
resting on a flat surface.
determines the outcome of a throw.
Some tetrahedron dice are numbered centrally along each base line and
are read by taking the numbers in the upright position along the base
resting on a flat surface. 

 Icosahedrons have 20 faces and each face is an equilateral triangle.
Opposite faces usually add up to 21.
Icosahedrons have 20 faces and each face is an equilateral triangle.
Opposite faces usually add up to 21.

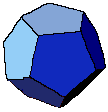
 Prisms don't make fair dice because top and bottom faces
are of a different shape and size to the rectangular ones but Prism dice have been
manufactured and you may come across them from time to time.
Prisms don't make fair dice because top and bottom faces
are of a different shape and size to the rectangular ones but Prism dice have been
manufactured and you may come across them from time to time. 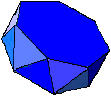 Anti-Prisms don't make fair dice because the top and bottom faces are of a
different shape and size to the triangular ones. You are unlikely to find a die of
this precise shape but you are likely to find their duals - Trapezohedra (see
below) and rolling log type Anti-Prisms modified with tapered ends (see
Anti-Prisms don't make fair dice because the top and bottom faces are of a
different shape and size to the triangular ones. You are unlikely to find a die of
this precise shape but you are likely to find their duals - Trapezohedra (see
below) and rolling log type Anti-Prisms modified with tapered ends (see

 The standard d8 commonly found in games retailers is a Dipyramid as
well as a Regular Polyhedron. Other Dipyramid dice are commercially
manufactured with more sides and can be found. In theory there are
an infinite number of possible Dipyramid shapes.
The standard d8 commonly found in games retailers is a Dipyramid as
well as a Regular Polyhedron. Other Dipyramid dice are commercially
manufactured with more sides and can be found. In theory there are
an infinite number of possible Dipyramid shapes. 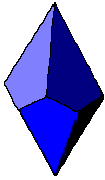
 The standard d10 commonly found in games retailers is a Trapezohedra
and so is the Regular Polyhedron the d6 Cube. The d10 Trapezohedra
usually has odd numbers on one side of the equatorial line and even
numbers on the other. d10s are usually numbered from 0 to 9 or 00 to
90 and not starting from 1 with 0 read as 10 in many applications. Traphezohedra with
more sides are commercially manufactured and can be found. In theory
there are an infinite number of Trapezohedra shapes. .
The standard d10 commonly found in games retailers is a Trapezohedra
and so is the Regular Polyhedron the d6 Cube. The d10 Trapezohedra
usually has odd numbers on one side of the equatorial line and even
numbers on the other. d10s are usually numbered from 0 to 9 or 00 to
90 and not starting from 1 with 0 read as 10 in many applications. Traphezohedra with
more sides are commercially manufactured and can be found. In theory
there are an infinite number of Trapezohedra shapes. .
 that uncommon and you may find them marked in a
variety of ways. Sometimes just marked 1 to 30
that uncommon and you may find them marked in a
variety of ways. Sometimes just marked 1 to 30
 This is a four-faced
regular Tetrahedron that's been pulled and
stretched out. Dice of this shape make fair dice and have been manufactured for RPGs
and CDGs.
This is a four-faced
regular Tetrahedron that's been pulled and
stretched out. Dice of this shape make fair dice and have been manufactured for RPGs
and CDGs.